토리첼리의 정리: 원리와 응용의 이해
목차
1. 토리첼리의 정리란?
이탈리아의 물리학자 에반젤리스타 토리첼리(Evangelista Torricelli)의 이름을 딴 토리첼리의 정리(Torricelli’s theorem)는 유체 역학의 기본 원리다. 이 정리는 오리피스에서 흘러나오는 유체의 속도와 개구부 위의 유체 높이 사이의 관계를 제공한다. Torricelli의 정리를 이해하는 것은 공학, 물리학 및 환경 과학의 다양한 응용에 매우 중요하다. 이 글에서는 Torricelli의 정리, 수학적 공식화 및 실제 적용의 이면에 있는 원리를 살펴본다.
2. 토리첼리 정리의 원리
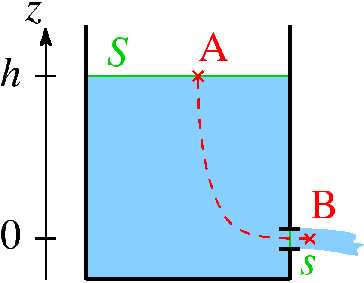
토리첼리의 정리(Torricelli’s theorem)에 따르면 중력 하에서 탱크 바닥에 있는 오리피스를 통과하는 유체의 유출 속도 \(v \)는 다음과 같이 주어진다.
\[ v = \sqrt{2gh} \]
이때
– \( v \)는 오리피스에서 나가는 유체의 속도.
– \( g \)는 중력으로 인한 가속도(지구에서는 대략 \( 9.81 \, m/s^2 \)).
– \( h \)는 오리피스 위 유체 기둥의 높이.
이 정리는 흐르는 유체의 압력, 속도 및 높이와 관련된 베르누이의 원리에서 파생된다. Torricelli의 정리는 유체가 작은 구멍을 통해 탱크에서 나가는 특정 시나리오에 Bernoulli의 원리를 적용하는 것을 단순화한다.
3. 수학적 파생
Torricelli의 정리를 도출하기 위해 Bernoulli의 방정식으로 시작한다.
\[ P_1 + \frac{1}{2} \rho v_1^2 + \rho gh_1 = P_2 + \frac{1}{2} \rho v_2^2 + \rho gh_2 \]
탱크 표면(점 1)과 오리피스(점 2)에 정지해 있는 유체에 대해 다음과 같이 가정합니다.
– 표면에서의 속도 \( v_1 = 0 \) (표면적이 오리피스 면적보다 훨씬 크기 때문에),
– 두 지점의 압력은 대기압 \( P_1 = P_2 \)이며,
– 오리피스의 높이 \( h_2 = 0 \).
이러한 가정하에 베르누이 방정식을 단순화하면 다음과 같은 결과를 얻습니다.
\[ \rho gh_1 = \frac{1}{2} \rho v_2^2 \]
\( v_2 \)를 풀면 다음을 얻습니다.
\[ v_2 = \sqrt{2gh_1} \]
이는 오리피스를 빠져나가는 유체의 속도고, 토리첼리의 정리의 유도 과정이다.
4. 실용적인 적용
4.1 엔지니어링
공학에서 Torricelli의 정리는 탱크, 저수지, 배수로 등 유체 배출과 관련된 시스템을 설계하고 분석하는 데 사용된다. 예를 들어, 수력공학에서 이 정리는 댐과 저수지의 물 흐름 속도를 계산하여 효율적인 물 관리와 홍수 조절을 보장하는 데 도움이 된다.
4.2 환경 과학
환경 과학자들은 Torricelli의 정리를 사용하여 자연 수역의 행동을 모델링합니다. 강과 하천의 유속을 이해하는 것은 환경 변화의 영향을 예측하고 수자원을 지속 가능하게 관리하는 데 필수적이다.
4.3 의료 기기
의료 분야에서는 토리첼리의 정리(Torricelli’s theorem)가 정맥(IV) 점적 주입과 같은 장치 설계에 적용됩니다. 이 정리는 환자에게 수액을 투여해야 하는 속도를 결정하여 정확하고 제어된 약물 전달을 보장하는 데 도움이 된다.
5. 결론
토리첼리의 정리는 유체 역학의 초석이며, 다양한 상황에서 유체의 거동을 이해하고 예측하기 위한 간단하면서도 강력한 도구를 제공한다. 그 응용 분야는 공학부터 환경 과학, 의학까지 다양한 분야에 걸쳐 있다. 전문가들은 Torricelli의 정리 원리를 숙지함으로써 보다 효율적인 시스템을 설계하고, 천연 자원을 보다 효율적으로 관리하며, 의료 치료를 개선할 수 있다. 이 정리를 이해하면 유체 역학에 대한 지식이 향상될 뿐만 아니라 실제 문제를 해결할 수 있는 실용적인 기술도 갖추게 된다.
물론 열심히 공부해서 적용해야하지만 ㅋㅋ …

